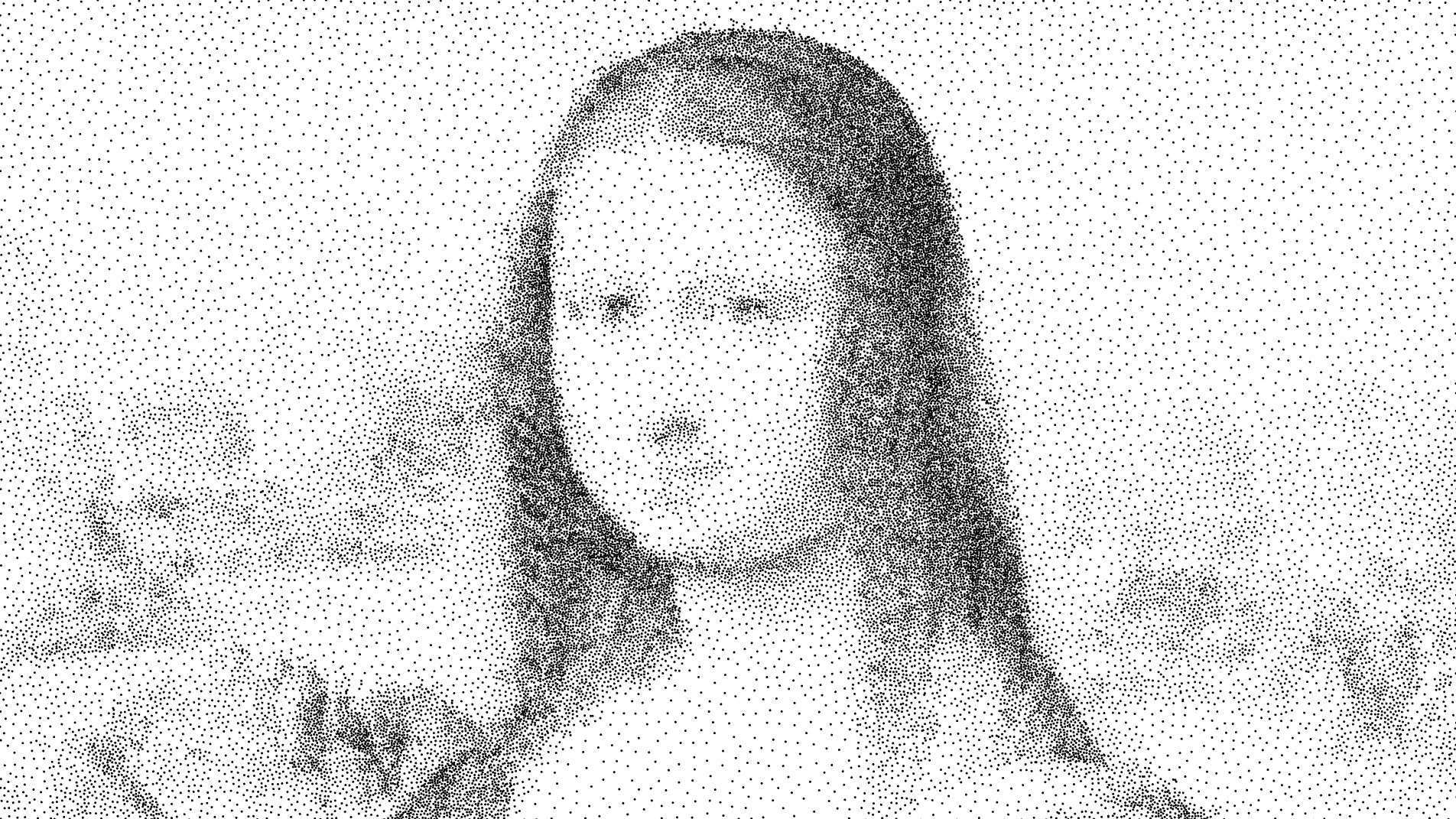COORD Cards - Poisson Sampling

A few years back I won a trip to attend the Shenzhen Maker Faire after placing first in a global embedded hardware contest on hackster.io. This gave me an opportunity to create something I had been wanting to tackle for some time: custom branded business cards. After all, if I was going to be making contacts at a popular tech event why not hand out striking cards with something bit more memorable than just my name on them?

For my cards I wanted to take advantage of a specific feature from Rhode Island print company called Moo called “Printfinity” that allows for all 50 cards in a pack to have their own unique design. Now, making 50 different iterations of my personal logo by hand would be unreasonable so it presented the perfect excuse to procedurally generate as many unique and beautiful cards as I needed with minimal repeated effort.

There are a number of neat algorithms that I have wanted to explore over the years but due to the pack limit I settled on the top 5, giving each flavor 10 cards of their own. The first algorithm we will explore here is inspired by natural phenomenon and has a number of creative applications, which makes it all the more interesting.

Now, just to preface the rest of this article: This isn’t a digital image sampling 101 lecture. As interesting as image processing algorithms can be, my usage of the algorithm described below is non-standard and seeks to display its pleasing appearance rather than its utility. If you want to know more about the nitty-gritty of disk sampling implementation and efficiency, please check out the sources cited at the bottom of the page.

Poisson Disk Sampling

Described as a sampling algorithm for computer graphics, Poisson Disk Sampling mimics the even-yet-scattered distribution of photoreceptor cells along the inner wall of primate retinas. This non-regular pattern of cells was suggested as a way to reduce spatial aliasing (jaggies) during rendering or image resampling operations. By swapping out a grid of samples (not unlike a standard computer monitor’s pixels) with a sample pattern that is somewhat randomized over the space to sample, you can eliminate numerous aliasing effects. Best described by Robert Cook in his seminal paper, this method effectively trades “highly objectionable artifacts (aliasing) […] with an artifact that our visual systems tolerate very well (noise).”¹

Comb of triangles rendered with 16 samples. Grid sampling (left), jittered sampling (right).

Figure 12 excerpt. Stochastic Sampling in Computer Graphics.

Instead of taking fully randomized samples over the coordinate space, which might sample one area repeatedly and others not at all, Poisson Disk Sampling adds one more condition: samples must be “placed with the restriction that no two samples are closer together than a certain [specified] distance.”¹ This spreads sample points out across the space with a regular density that is not-unlike the biological distribution of cells seen within the eye of a macaque monkey!⁴

Macaque cone cell distribution (right) versus output of Bridson's Poisson algorithm (left), implemented in processing.

Adapted from "Non-fluorescent dye staining of primate blue cones", Figure 2

The algorithm’s original implementation description admits that despite its fantastic sampling results, it is just too expensive for most image sampling tasks.¹ As time progressed, faster implementations have been developed yet still remain weak in comparison to competing methods such as Jittered Grids or Sobol Sequences. Still, this hasn’t stopped developers from taking the idea of what the algorithm generates and applying it in creative (and less resource-restrictive) situations.

Pleasing Irregularity

My first exposure to Disk Sampling was a 2008 article from South African gamedev magazine Dev.Mag.³ It offered a straightforward demo implementation of Bridson’s Fast Poisson Disk Sampling² algorithm for non-real time applications like object placement and texture generation. Even though Disk Sampling isn’t a reasonable method for performing image resampling, it still generates fantastically organic patterns for spawning flora on videogame maps⁵ or replicating natural phenomena like condensation on the outside of a cool window.

After popping open a processing editor and grappling with a few out-of-bounds errors, I had a functional implementation of Bridson’s algorithm generating patterns of dots that eerily matched those images of dyed primate eye cells! Swapping the code around to draw the list of valid samples as points get added yielded this pleasing growth animation as dots spread out over the screen; scattered in their placement but still constrained by their distances to one another. If you pay close attention, you can even see a few instances where sample points fill in little gaps in areas that are already well populated.

At neat as it looked, there wasn’t that much variety between runs. Even with a few attempts at selective color patterns tied to point location or list index (as shown above), it was much too homogenous. Now each point in the vanilla implementation is restricted by how close they can be placed to existing points, but nothing was limiting the code from making that minimum distance a variable. Paying attention to the underlying reasoning behind Bridson’s algorithm (namely the size of the acceleration grid for point searches), you can vary that minimum distance using other data sources. This change makes for some interesting applications such as generating unique stipple-shaded artworks from existing images.

Stippling effect created via minimum distance driven by the brightness of an image's pixels.

Click the image for full resolution.

Processing provides an easy to use Perlin noise function (which I’ve used for other cards, see COORD Cards - Perlin and Simplex to read more) that proved to be a fantastic source of continuous, dynamic looking gradients that take those flat-looking dots and gives them depth. By slowly varying the minimum distance between points and the visual size of each point with the noise values, subtle peaks and valleys form over the span of the image.

Poisson Disk Sampling with the minimum distance scaled by Perlin noise.

Finishing Touches

For the last additions, the color of each point generated via the sampling algorithm was determined by either the Perlin noise value (higher values yielding lighter greys) or the color of an image consisting of the COORD logo with a transparent background; if the logo image’s pixel below the generated point was transparent, it would use the noise-generated color, otherwise it would take the COORD color tones from the image. This made the final works consistent with the COORD branding and made the variable minimum distance more apparent by adding a sense of depth with the rising and falling gradients.

To show how the overall sample pattern is created, I swapped the search method for Bridson’s algorithm from breadth-first-search to depth-first-search to form long, winding chains of points that crawl over the span of the image. As valid sample points were added to the list, lines connecting each successive point would show the path of the algorithm as it seeks to fill every open space in the image by first following one chain of possibilities until a dead end is found then doubling back.

Compare the first growth animation above to the final piece below. All those small adjustments combine to create something very interesting to watch in an animated form that looks equally striking when printed to a glossy, static card.

By varying the Perlin noise seed with each run of the processing sketch, unique cards get generated in a fraction of a second; each following the same geometric and visual rules but with satisfyingly different outcomes. The variations are especially apparent on the bright-colored logo, where changes in density work to define or decimate the infill of each letter within the thin outline.

Click the image for full resolution.

Final Notes

Overall, I am really pleased with how these came out. From the initial implementation to its final appearance, the process was natural and serendipitous; continually generating visual possibilities (like procedural stippling!) that deserve more attention. Best of all, the final cards carry the quickly-recognizable branding but still offer a wealth of visual complexity for anyone that gives them a good look.

Be sure to check out the other designs from this series:

COORD Cards - Perlin and Simplex

Sources

1. Cook, Robert. (1986). Stochastic Sampling in Computer Graphics. ACM Trans. Graph.. 5. 51-72. 10.1145 / 7529.8927.

2. Bridson, Robert. (2007). Fast Poisson disk sampling in arbitrary dimensions. ACM SIGGRAPH. 10.1145 / 1278780.1278807.

3. Tulleken, Herman. “Poisson Disk Sampling.” Dev.Mag Issue 21, Mar. 2008, web.archive.org/web/20160707105240/http://devmag.org.za/2009/05/03/poisson-disk-sampling/

4. E P McCrane, F M de Monasterio, S J Schein, R C Caruso; Non-fluorescent dye staining of primate blue cones.. Invest. Ophthalmol. Vis. Sci. 1983;24(11):1449-1455.

5. Lague, Sebastian. “[Unity] Procedural Object Placement (E01: Poisson Disc Sampling).” YouTube, YouTube, 23 Nov. 2018, www.youtube.com/watch?&v=7WcmyxyFO7o.